
We present PyMoiré, a computational framework for generating and optimizing moiré patterns in twisted bilayer and multilayer two-dimensional materials. Our approach introduces a novel elastic energy minimization scheme that accurately captures the strain distribution between layers, providing significant improvements over traditional geometric matching methods. The framework particularly excels in handling materials with different elastic properties, making it valuable for studying heterogeneous material combinations such as transition metal dichalcogenides (TMDs).
The discovery of novel physical phenomena in twisted bilayer systems has sparked intense research interest in moiré materials. However, identifying optimal stacking configurations that balance strain energy with desired periodicities remains a significant challenge. PyMoiré addresses this challenge by providing a systematic approach to generating moiré patterns while considering the elastic properties of the constituent materials.
The framework begins with the specification of base materials through their lattice vectors and stiffness tensors. For a given twist angle θ, our LatticeMatcherExplicit algorithm identifies potential matching points between the layers in both crystallographic and Cartesian coordinates. This initial geometric matching serves as the foundation for subsequent optimization.
We implemented three distinct approaches to determine the optimal moiré configuration:
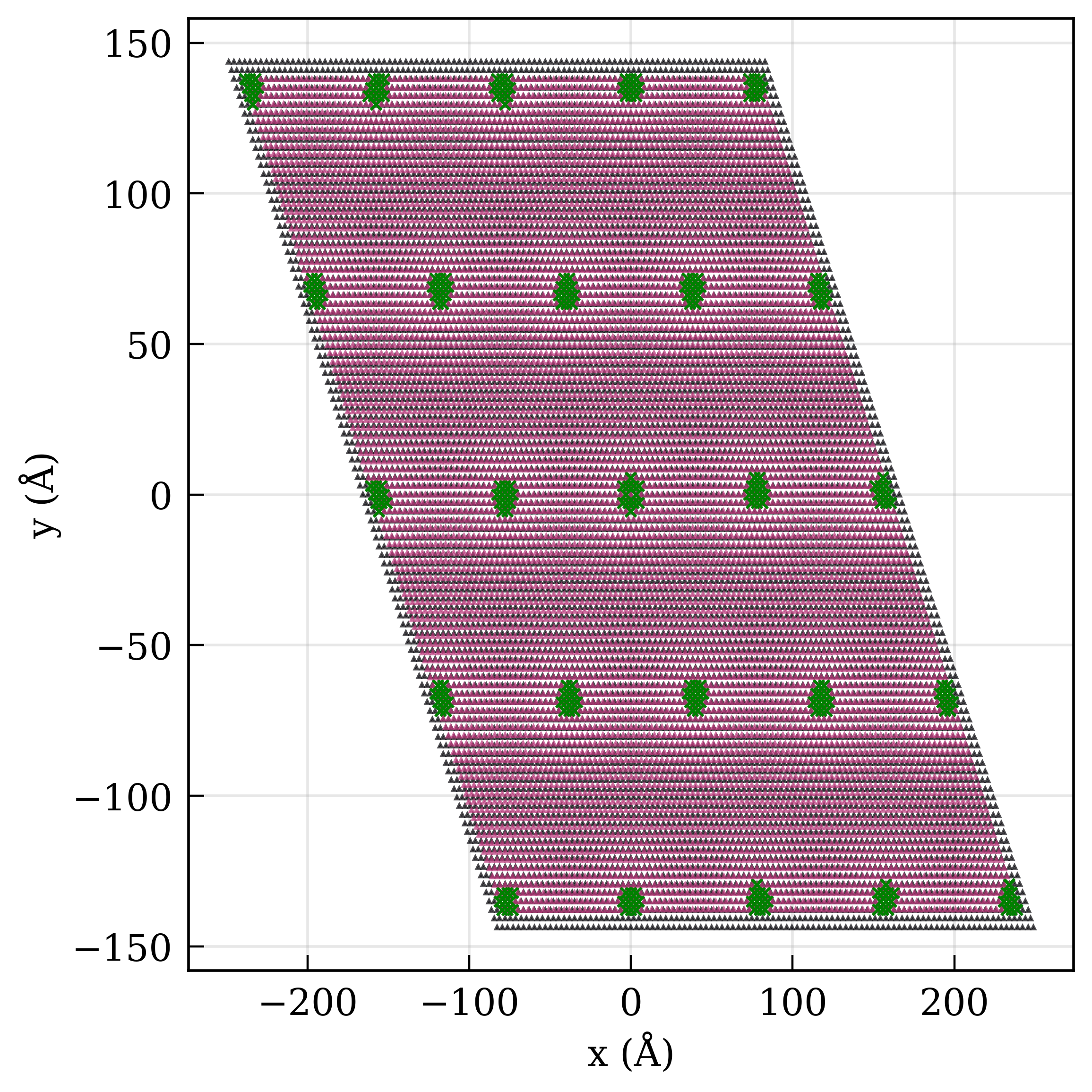
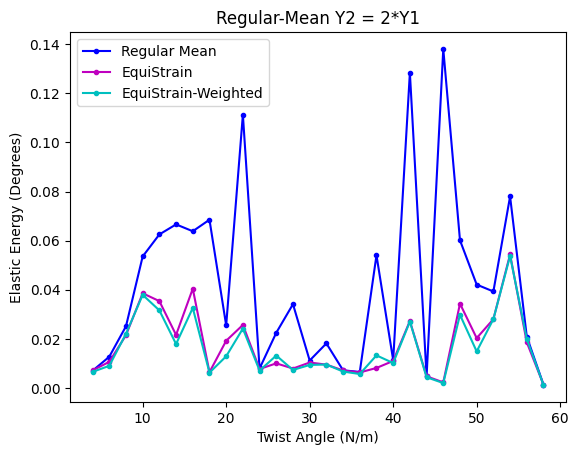
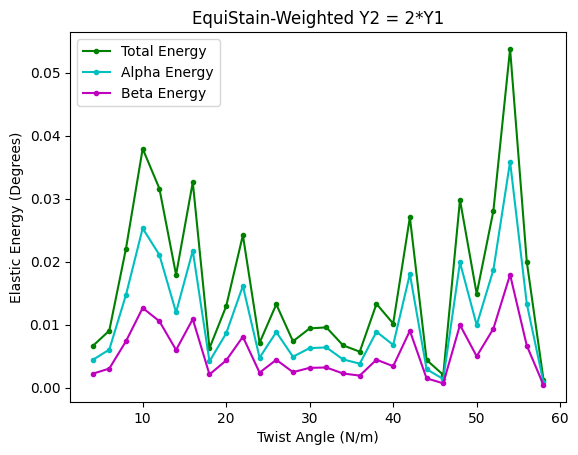
Our implementation shows significant improvements in physical accuracy compared to traditional geometric approaches. For the MoS₂/MoSe₂ system, the weighted EquiStrain method demonstrates optimal strain distribution between layers, particularly when the Young's moduli of the materials are similar.
The current implementation has several known limitations:
Ongoing work focuses on:
PyMoiré represents a significant advance in the computational modeling of moiré systems. By incorporating elastic energy considerations into the pattern generation process, we enable more physically accurate predictions of stable configurations in twisted bilayer systems. This tool provides researchers with a powerful framework for exploring the vast parameter space of possible moiré structures, accelerating the discovery of novel material systems with desired properties.
We thank our collaborators and the broader 2D materials community for their valuable feedback and suggestions during the development of PyMoiré.

the lovely people of the Jornada group (a picture taken before I joined)